Note of Alloy Analyzer
- Author: chew.y.feng@outlook.com
- Date: 03/29/2024
Introduction
This note is a brief summary of Alloy for SWEN90010, Unimelb.
Alloy is an analyzer for software modeling. This subject mainly uses Alloy to find holes in security mechanisms. To be more specific, we use Alloy to prove properties about the software specification, such as safety and security.
Propositional Logic
Alloy support basic propositional Logic:
all city : AustralianCities | Raining[city]
It says “for all cities in Australia, they are raining”
Relation and Predicates
Everything is a relation in Alloy. Sets are just unary relations. e.g.
Username = {(U0), (U1), (U2)}
URL = {(UR0), (UR1), (UR2)}
Password = {(P0), (P1), (P2)}
For arity > 1, relations are also sets e.g.
Factor(x,y,z) — {(x,y,z) | x = y * z}
In summary, we have Sets = Relations = Predicates in alloy
Operators
Set operators

Relation operators
Username = {(U0, U1, U2)}
Password = {(P0, P1, P2)}
// cross product
Username->Password = { (U0, P0), (U0, P1), (U0, P2),
(U1, P0), (U1, P1), (U1, P2),
(U2, P0), (U2, P1), (U2, P2)}
urlPasswords = {(U0, UR0, P1), (U0, UR1, P2), (U1, UR0, P2)}
myUsername = {(U0)}
myUrl = {(UR1)}
myPassword = {(P2)}
// dot join
myUsername.urlPasswords = { (UR0, P1), (UR1, P2) }
// box join
myUsername.urlPasswords[myUrl] = {(P2)}
// domain restriction
urlPasswords <: myUsername = {(U0, UR0, P1), (U0, UR1, P2) }
// range restriction
urlPasswords :> myPassword = {(U0, UR1, P2), (U1, UR0, P2)}
// override is defined as A ++ B = (A - (domain[B] <: A) + B)
updatedPassword = {(U0, UR0, P3)}
urlPasswords ++ updatedPassword = {(U0, UR0, P3), (U0, UR1, P2), (U1, UR0, P2)}
// cardinalities
#urlPasswords = 3
Note that if the relation has an arity of n, the first (n-1) are seen as domain, the last one is the range.
Propositional Logic Operators
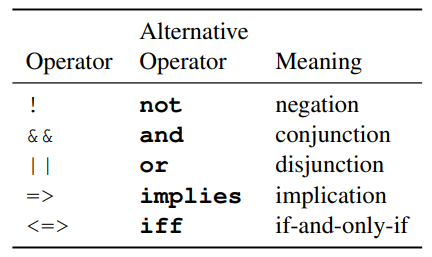
Quantifiers
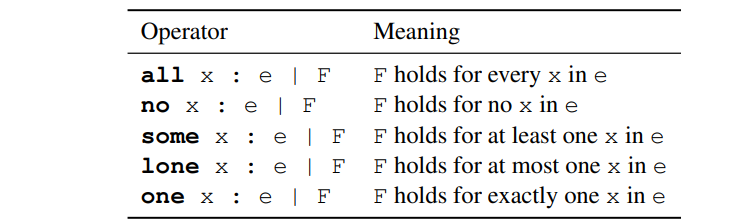
The last four can also be used to declare sets.
Temporal Logic
One major feature of Alloy is that it can reason about temporal logic by temporal operators.
Temporal Logic
Alloy adopts a model-based specification system, in which the system is defined as a state machine model. In an abstract state machine model, the state e volves over time
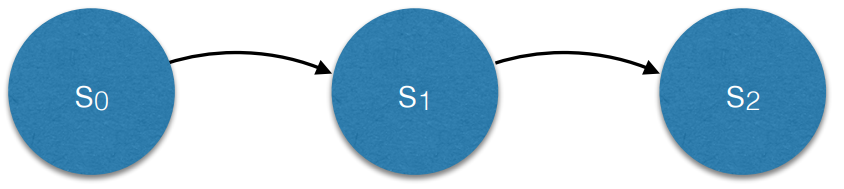
We can describe the transition as preconditions (what the state should satisfy before the transition) and postconditions (constraints after the transition).
For safety and security properties, we typically want it to hold in all states. Thus, it is called a state invariant.
To prove a state invariant inv, we need to use induction:
(a) inv holds in the initial state
(b) For each operation op_i, if inv holds in states, inv still holds after the operation op_i.
Language
There are two ways to express things happen in a timeline:
(a) Use the next state operator ' for sets
newPassword = updatedPassword = {(UR0, P3)}
user.passwords’ = user.passwords ++ newPassword
It says “In the next state, there is one password being updated”
(b) Use temporal logic keywords for predicates
// after means the predicate holds for next state on the timeline
delete_all[user] => after (no user.passwords)
 All temporal operators
All temporal operators
Alloy Language
Signatures are type declarations.
 Common Signature Declarations
Common Signature Declarations
Example: Passbook is a database that stores the relation of (user, url, password).
sig URL {}
sig Username {}
sig Password {}
sig PassBook {var password : Username -> URL -> Password}
Facts are constraints that are assumed to hold true. They only check initial state by default , unless there are temporal keywords.
fact NoDuplicates
{
always all pb : PassBook, user : Username, url : URL
| lone pb.password[user][url]
}
It reads “for all time, all passbooks, users and URLs, there is at most one password for each (user,url) pair”
Predicates are primarily used to introduce operations over a state
//Add a password for a new user/url pair
pred add [pb : PassBook, url : URL, user: Username, pwd: Password] {
no pb.password[user][url]
pb.password’ = pb.password + (user->url->pwd)
}
//Delete an existing password
pred delete [pb : PassBook, url : URL, user: Username] {
one pb.password[user][url]
pb.password’ = pb.password - (user->url->Password)
}
Functions are named expressions for reuse of code
//Return the password for a given user/URL pair
fun lookup [pb: PassBook, url : URL, user : Username] : lone Password {
pb.password[user][url]
}
Assertions are constraints are we want to check. We primarily use them to express the safety or security properties
// (durability) If we add a new password,
// then we get this password when we look it up
assert addWorks {
all pb : PassBook, url : URL, user : Username, p : Password |
add [pb, url, user, p] => (after (lookup [pb, url, user]) = p)
}
Model Checking
The advantage of Alloy is that proofs are automated. Users only need to give the constraints, then Alloy would try to find a counterexample. This approach significantly reduces the efforts in writing proofs. But the tradoff is that it cannot guarantee completeness.
Example:
assert lone_password_per_user_url {
all pb, user, url, pwd, res |
(all user1, url1 | lone pb.password[user1][url1]) and
no pb.password[user][url] and
pb.password’ = pb.password + (user->url->pwd) =>
(lone pb.password’[user][url])
}